The challenge takes place at September 27th. Please find a detailed list of the schedule and a link to all accepted papers at our workshop section.
Category Archives: Blog
We are curiously awaiting your paper submissions
As the offline challenge has ended and the online challenge not yet started, we had a short look at your submitted result files. Though we only saw what was recommended, we already know that completely different approaches for the name recommendation task were applied. So we are very much looking forward to reading your papers and getting an impression of all the different pre processing and recommendation systems.
After passing the reviewing process, all papers of participants of the challenge’s workshop will be published in the workshop proceedings (for details, have a look at the workshop description). The workshop will take place on September 27th, that is, on the last conference day.
The introduction of the workshop proceedings will contain an introduction to the overall setup of the challenge as well as a detailed task description. You can therefore skip these details in your paper and just refer to the introduction.
If you have further questions concerning your workshop submission, please don’t hesitate to contact us.
Happy letter typing!
11th Leaderboard
A new team rushed to the top of our leaderboard. Close behind is team disc who improved their score every week since they started on the leaderboard. With this speed of progress, they will be on top of the leaderboard until next week. We are waiting the next recommender result submission for the coming leaderboard.
| Pos | Diff | Team Name | Score |
|---|---|---|---|
| 1 | all your base | 0,0357 | |
| 2 | disc | 0,0324 | |
| 3 | Context | 0,0318 | |
| 4 | TomFu | 0,0309 | |
| 5 | sertão | 0,0296 | |
| 6 | Labic | 0,0291 | |
| 7 | ibayer | 0,0259 | |
| 8 | cadejo | 0,0200 | |
| 9 | thalesfc | 0,0199 | |
| 10 | TeamUFCG | 0,0156 | |
| 11 | PwrInfZC | 0,0130 | |
| 12 | persona-non-data | 0,0043 |
Teaser #4: Namelings and ReTweet Links
Once again we have some nice results to share! Today we look at Twitter’s ReTweet graph, based on the same data set which was described in Teaser #3. The ReTweet graph was extracted from Jure Leskovec’s Twitter Sample, applying a simple RT @username filter (thereby ignoring “dark retweets”).
The resulting ReTweet graph comprises 826,104 users with 2,286,416 edges. Just considering the ReTweet frequencies (i.e., how often user A retweeted user B), we aggregated some average similarity scores. Firstly, we collected all hash tags for each user separately and represented the user by the resulting hash tag context vector (i.e. each component of a user’s context vector contains the number of tweets in which the user applied the corresponding hash tag). Thus we can calculated the cosine similarity between pairs of users, based on the corresponding context vectors. Averaging these similarity scores per retweet frequency, we obtained the following plot (excluding self retweets):
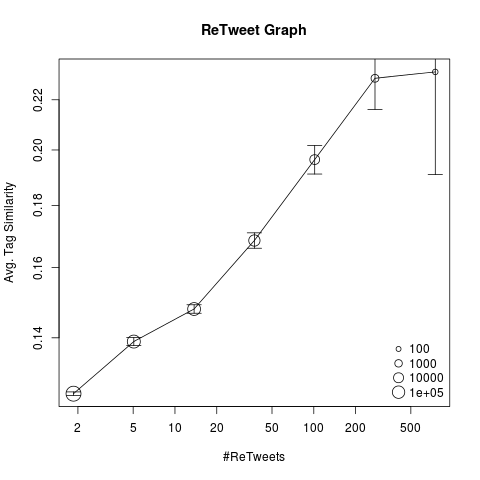
As we can see: Pairs of users who retweet one the other more frequently, tend to be more similar with respect to the corresponding hash tag usage. This is not surprising, but nevertheless, nice to see. Please note that the plots are log-log scaled and retweet freqencies are binned logarithmically.
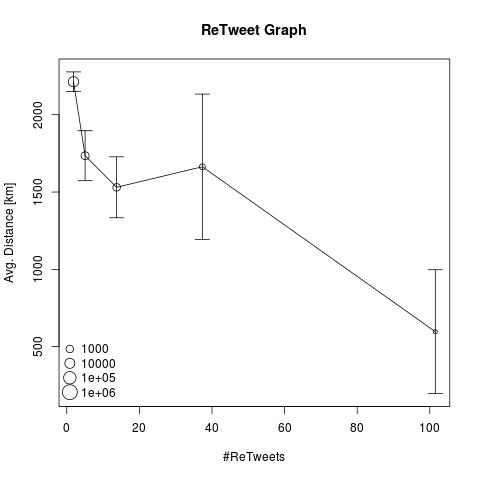
Secondly, we extracted geo locations for Twitter users and calculated the average geographic distance of user pairs, relative to the corresponding retweet count:
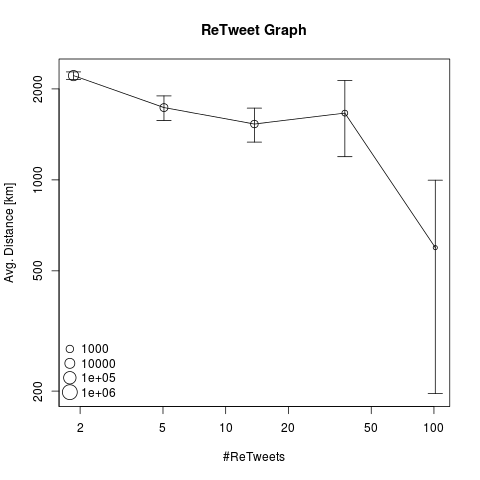
These results are not as clear as in the case of hash tag similarity, but nevertheless, we can observe the tendency of user pairs with higher retweet counts being more closely located. It is worth noting that the global average geographic distance of all users is 7,484 Kilometres and thus already low retweet frequencies yield significantly lower average distances. For your convenience, we also show the linear scale plot:
But finally, the interesting part: Again, we heuristically determined given names for Twitter users by matching the user name with our list of known names. We thus collected names for 179,260 users, having 111,204 links in the ReTweet graph (excluding self retweets). We than calculated the average name similarity of user pairs based on the name co-occurrence graph derived from the English Wikipedia corpus (as described in the Nameling papers):
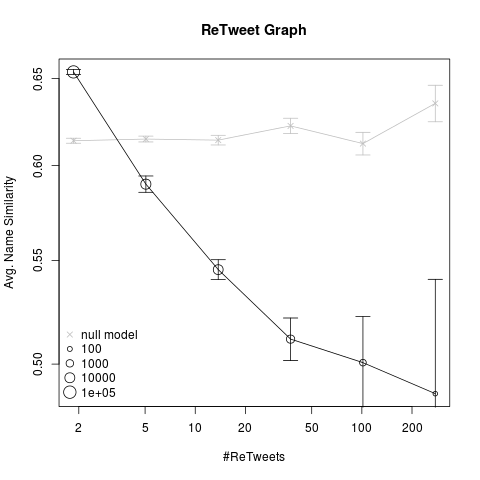
The result is rather unexpected: The average name similarity decreases with increasing retweet counts! That is, spontaneous retweets are more likely among users with similar names and user pairs which retweet often tend to have less similar names.
At this point, further investigation is due. Maybe these results are artefacts induced by the applied name similarity function. But other hypothesis may also support these observations. Higher average name similarity for low retweet counts can be explained by assuming that spontaneous retweets are more likely related to topics which are relevant to the retweeting user’s cultural background (e.g. local events, TV shows, etc.) and for user pairs who retweet often, the name correlated relations are less important, as these users share some focused interest (e.g. Recommender Systems).
These are of course only speculations and we welcome you to discuss these observations either via Twitter or in our forum!
Happy number crunching!
2nd Leaderboard
Nothing changed this week since there where no new result submissions. We are waiting for your recommender result submission for the next leaderboard which will be online on April 12th.
| Pos | Diff | Team Name | Score |
|---|---|---|---|
| 1 | TeamUFCG | 0,0262 | |
| 2 | TomFu | 0,0158 |
Leaderboard
Our first baby name heroes are team TeamUFCG and TomFu. We are waiting for your recommender result submission for the next leaderboard which will be online on April 5th.
| Pos | Diff | Team Name | Score |
|---|---|---|---|
| 1 | TeamUFCG | 0,0262 | |
| 2 | TomFu | 0,0158 |
Teaser #3: I follow whom my name is alike
Once again, it’s time for some number crunching fun… Today, I looked at the interrelationship of first names within Twitter’s Follower graph and got some beautiful results.
For the analysis, I used an excerpt of the Follower graph, consisting of 1,486,403 users and 72,590,619 links (as described here), as well as the name co-occurrence graph based on the English Wikipedia corpus which is used for calculating name similarities in Nameling (as described in the Nameling papers). The fist names of Twitter users were extracted from the users’ profile data, where a user may provide her or his full name. Of course, many users just entered some fantasy name. Accordingly, the first token of the provided name string which matched against our list of known names was chosen as the user’s first name. This process induces some noise into the data, but due to the vast number of considered pairs of users, this effect should be neglectable.
Now, relative to 3,078 randomly chosen users (our Linux cluster is still crunching on more), I calculated the average name similarity of direct neighbours in the Follower graph, the average name similarity between pairs of users at a (shortest path) distance of two, …of three, and so on. For reference, I also added the total average name similarity for all considered pairs of users, as depicted by the grey dashed line. Finally, the error bars correspond to the 95% confidence interval.
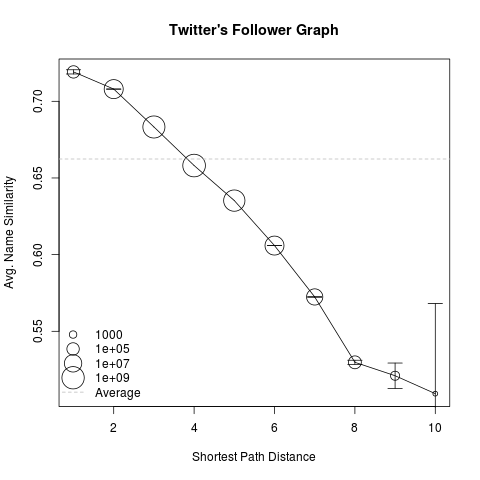
As we can see, users which are located more closely within the follower graph tend to have more similar names than distant users. Additionally, a monotonically decreasing dependency between the average name similarity and the shortest path distance in the follower graph can be observed. Moreover, users at a distance up to three tend to have more similar names than in average, whereas users with shortest path distances above three tend to have less similar names than in average.
Stay tuned for more results (eg. considering the ReTweet graph and ReTweet frequency) and happy number crunching!
Teaser #2: Given Names and the Co-Authorship Relation
Science is universal, independent of cultural prejudices and political boundaries – and of course, independent of an author’s name. Or not? Try calculating the average similarity of your name with all of your co-authors’ names, and the average name similarity with your co-authors’ co-authors, and so on.
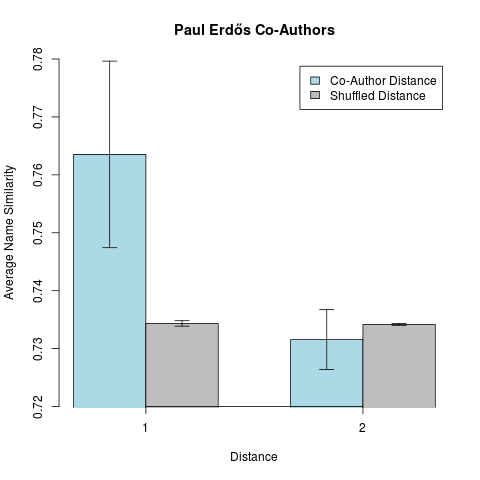
We did these calculations for the Paul Erdős’ collaboration network. Paul Erdős is known for having published papers with more collaborators than any other mathematician (the considered collaboration network counts 572 direct collaborators and 6383 at distance two). For reference, we additionally calculated the average name similarity for 1000 randomly relabled collaboration networks (keeping Paul Erdős’ node fixed), as depicted in grey on the plot below. The given error ranges correspond to the 95% confidence interval.
First of all, we note only a small difference in magnitude for the average name similarity at distance 1 and distance 2. Nevertheless, considering the 95% confidence interval, even for Paul Erdős, the tendency of co-authors having more similar names, can not be neglected. For co-authors at distance 2, author names even exhibit the very slight tendency of being less similar than according randomly chosen co-authors.
Of course, we must take care to avoid the confusion of correlation and causality. Giving your child the name “Paul” won’t increase the probability of collaboration with Paul Erdős (especially as he unfortunately already died in 1996). Nevertheless, considering your own collaboration network, more astonishing results may be observed…
P.S.: The name “Paul” by itself is special, as it is one of the most popular names in Wikipedia and accordingly, more related to other names as the average name is. The impact of the source name’s distributional properties can be ignored, by calculating the pairwise average name similarity at distance k separately. In case for Paul Erdős, the direct co-authors’ names have an average pairwise similarity score of 0.64 in contrast to 0.51 at distance two (estimated, as the calculation hasn’t finished yet).
Teaser #1: How similar are your friends’ names?
Try calculating the overall average similarity of names (e.g. based on co-occurrences in Wikipedia) and the average similarity of you and all your friends’ names. Do these average similarity scores differ significantly?
Here are the results for the 20DC13 Team
Firstly, our team members’ first names are Stephan, Andreas, Robert, Folke and Jürgen (ordered alphabetically by the last name).
We constructed the name co-occurrence graph based on sentences within the English Wikipedia, as described in our papers. Each name can then be represented by its “context” vector, i.e., the corresponding row within the co-occurrence graph’s adjacency matrix. We then calculated the similarity between two names as the cosine similarity between the corresponding context vectors. (These is by the way the similarity which is implemented in nameling and is for the respective top 100 similar pairs of name available for download).
Well, here are the pair-wise similarity scores for the 20DC13 team:
| Name1 | Name2 | Similarity |
|---|---|---|
| Stephan | Andreas | 0.901121 |
| Stephan | Robert | 0.789887 |
| Stephan | Folke | 0.549801 |
| Stephan | Jürgen | 0.806095 |
| Andreas | Robert | 0.688174 |
| Andreas | Folke | 0.558555 |
| Andreas | Jürgen | 0.849864 |
| Robert | Folke | 0.465395 |
| Robert | Jürgen | 0.569373 |
| Folke | Jürgen | 0.474674 |
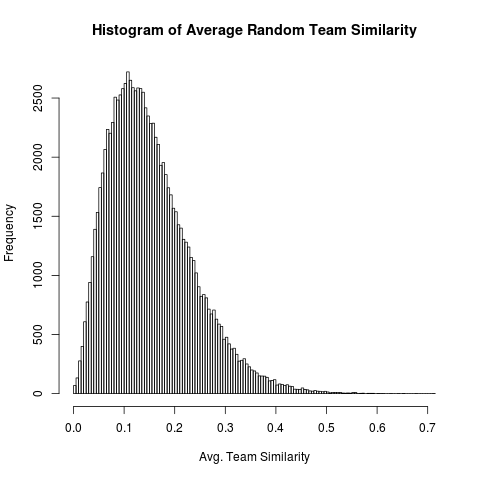
In average, our team member similarity score is accordingly 0.665294. The total average pair-wise similarity is 0.02914, so our team’s similarity score is more than 22 times above average. Additionally, we repeatedly selected random groups of names of the same size as our team (100,000 repetitions) and calculated the respective average group similarity, resulting in the following histogram:
So yes, our team’s average name similarity is significantly larger than expected by chance!
Happy number crunching!
.folke
Collaborative Bibliography
You find challenge-related publications on our new literature page. Contribution is open via BibSonomy. You will have to join the 20DC13 group.